Fractal River Basins Chance And Self-organization Pdf

Posted on by admin

A view of river basins 2. Fractal characteristics of river basins 3. Multifractal characteristics of river basins 4. Optimal channel networks: minimum energy and fractal structures 5. FRACTAL RIVER BASINS CHANCE AND SELF-ORGANIZATION. Fractal Characteristics of River Basins 99. 2.7 Self-Affinity in River Basins 145.

  1. Fractal River Basins Chance And Self-organization Pdf
  2. Fractal River Basins Chance And Self-organization Pdf Online
  3. Fractal River Basins Chance And Self-organization Pdf Free

Fractal River Basins: Chance and Self-Organization

Fractal River Basins: Chance and Self-Organization PDF TagsDOWNLOAD EBOOK Fractal River Basins: Chance and Self-Organization,Fractal River Basins: Chance and Self-Organization ebook download,Fractal River Basins: Chance and Self-Organization pdf online,Fractal River Basins: Chance and Self-Organization read online,Fractal River Basins: Chance and Self-Organization epub donwload,Fractal River Basins: Chance and Self-Organization download,Fractal River Basins: Chance and Self-Organization audio book,Fractal River Basins: Chance and Self-Organization online,read Fractal River Basins: Chance and Self-Organization,pdf Fractal River Basins: Chance and Self-Organization free download,ebook Fractal River Basins: Chance and Self-Organization download,Epub Fractal River Basins: Chance and Self-Organization,full download Fractal River Basins: Chance and Self-Organization by Ignacio Rodríguez-Iturbe,Pdf Fractal River Basins: Chance and Self-Organization download,Fractal River Basins: Chance and Self-Organization free,Fractal River Basins: Chance and Self-Organization download file,Fractal River Basins: Chance and Self-Organization ebook unlimited,Fractal River Basins: Chance and Self-Organization free reading,Fractal River Basins: Chance and Self-Organization audiobook download,Fractal River Basins: Chance and Self-Organization read and download,Fractal River Basins: Chance and Self-Organization for pc,Fractal River Basins: Chance and Self-Organization download for kindle,Fractal River Basins: Chance and Self-Organization ready for download,Fractal River Basins: Chance and Self-Organization free read and download trial 30 days,Fractal River Basins: Chance and Self-Organization save ebook,audiobook Fractal River Basins: Chance and Self-Organization play online,[PDF] DOWNLOAD Fractal River Basins: Chance and Self-Organization FOR IPAD - BY Ignacio Rodríguez-Iturbe

Book Details

Chance

Author : Ignacio Rodríguez-Iturbe

Pages : 565 pages

Publisher : Cambridge University Press 1997-06-13

Fractal River Basins Chance And Self-organization Pdf

Fractal river basins chance and self-organization pdf online

Language : English

Book Synopsis

Fractal River Basins Chance And Self-organization Pdf Online

River

Fractal River Basins Chance And Self-organization Pdf Free

  1. Al-Wagdany AS (1993) Geomorphologic characteristics and instantaneous unit hydrographs of Indiana watersheds: Dissertation, Purdue University, 177pGoogle Scholar
  2. De Bartolo SG, Gaudio R, Gabriele S (2004) Multifractal analysis of river networks: sandbox approach. Water Resour Res 40(2):1–10Google Scholar
  3. De Bartolo SG, Veltri M, Primavera L (2006) Estimated generalized dimensions of river networks. J Hydrol 322:181–191CrossRefGoogle Scholar
  4. Dimri VP (2005) Fractals in geophysics and seismology: an introduction. In: Fractal behaviour of the earth system. Springer, Berlin Heidelberg, pp 1–22Google Scholar
  5. Dimri VP, Vedanti N (2005) Scaling evidences of thermal properties in earth’s crust and its implications. In: Fractal behaviour of the earth system. Springer, Berlin Heidelberg, pp 119–131Google Scholar
  6. Dombrádi E, Timár G, Bada G, Cloetingh S, Horváth F (2007) Fractal dimension estimations of drainage network in the Carpathian–Pannonian system. Glob Planet Chang 58(1–4):197–213CrossRefGoogle Scholar
  7. Feder J (1988) Fractals. Plenum, New YorkCrossRefGoogle Scholar
  8. Fletcher JE, Huber AL, Haws FW, Clyde CG (1977) Runoff estimates for small rural watersheds and development of a sound design method: fed. Highway Adm., Report No. FHWA-RD-77-158Google Scholar
  9. Gaudio R, De Bartolo SG, Primavera L, Gabriele S, Veltri M (2006) Lithologic control on multifractal spectrum of river networks. J Hydrol 327(3):365–375Google Scholar
  10. Gray DM (1961) Interrelationship of watershed characteristics. J Geophys Res 66:1215–1223CrossRefGoogle Scholar
  11. Gregory KJ, Walling DE (1973) Drainage basin form and process. E. Arnold, LondonGoogle Scholar
  12. Hausdorff F (1919) Dimension und außeres Maß. Math Ann 79:157–179CrossRefGoogle Scholar
  13. Hjelmfelt AT (1988) Fractals and the river-length catchment-area ratio. Water Resour Bull 24(2):455–459CrossRefGoogle Scholar
  14. Horton RE (1945) Erosional development of streams and their drainage basins: hydrophysical approach to quantitative morphology. Geol Soc Am Bull 56:275–370CrossRefGoogle Scholar
  15. La Barbera P, Rosso R (1989) On the fractal dimension of stream networks. Water Resour Res 25(4):735–741CrossRefGoogle Scholar
  16. La Barbera P, Rosso R (1990) Reply. Water Resour Res 26(9):2245–2248Google Scholar
  17. Langbein WB (1947) Topographic characteristics of drainage basins: USGS Professional Papers 968-CGoogle Scholar
  18. Mandelbrot BB (1983) The fractal geometry of nature. Freeman, New YorkGoogle Scholar
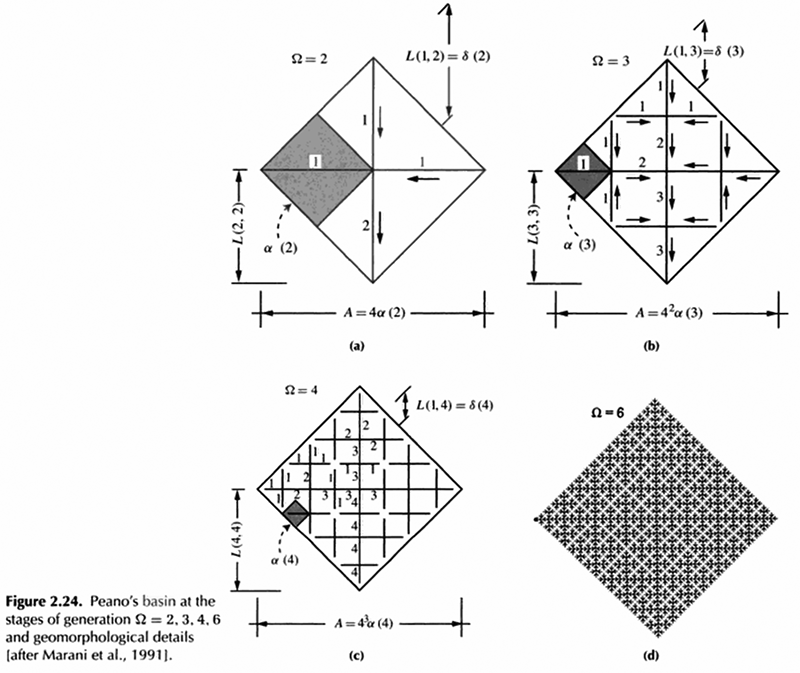
  19. Marani A, Rigon R, Rinaldo A (1991) A note on fractal channel networks. Water Resour Res 27(12):3041–3049CrossRefGoogle Scholar
  20. McDermott GE, Pilgrim DH (1982) Design flood estimation for small catchments in New South Wales: Australian Water Resources Council Technical Paper 73. Department of National Development, CanberraGoogle Scholar
  21. Mesa OJ, Gupta VK (1987) On the main channel length–area relationship for channel networks. Water Resour Res 23(11):2119–2122CrossRefGoogle Scholar
  22. Pawelzik K, Schuster HG (1987) Generalized dimensions and entropies from a measured time series. Phys Rev A 35(1):481–484CrossRefGoogle Scholar
  23. Pilgrim DH (1986) Bridging the gap between flood research and design practice. Water Resour Res 22(9):165S–176SCrossRefGoogle Scholar
  24. Rinaldo A, Rodriguez-Iturbe I, Rigon R, Bras RL, Ijjasz-Vasquez EJ, Marani A (1992) Minimum energy and fractal structures of drainage networks. Water Resour Res 28(9):2183–2195CrossRefGoogle Scholar
  25. Rodríguez-Iturbe I, Rinaldo A (2001) Fractal river basins: chance and self-organization. Cambridge University Press, New YorkGoogle Scholar
  26. Rosso R, Bacchi B, La Barbera P (1991) Fractal relation of mainstream length to catchment area in river networks. Water Resour Res 27(3):381–387CrossRefGoogle Scholar
  27. Schuller DJ, Rao AR, Jeong GD (2001) Fractal characteristics of dense stream networks. J Hydrol 243:1–16CrossRefGoogle Scholar
  28. Shreve RL (1966) Statistical law of stream numbers. J Geol 74:17–37CrossRefGoogle Scholar
  29. Strahler AN (1957) Quantitative analysis of watershed geomorphology. Trans Am Geophys Union 38:913–920CrossRefGoogle Scholar
  30. Takayasu H (1990) Fractals in the physical sciences. Manchester University Press, ManchesterGoogle Scholar
  31. Tarboton DG, Bras RL, Rodriguez-Iturbe I (1988) The fractal nature of river networks. Water Resour Res 24(8):1317–1322CrossRefGoogle Scholar
  32. Tarboton DG, Bras RL, Rodriguez-Iturbe I (1990) Comment on the fractal dimension of stream networks. Water Resour Res 26(9):2243–2244Google Scholar
  33. Telesca L, Lapenna V (2005) Fractal methods in self-potential signals measured in seismic areas. In: Fractal behaviour of the earth system. Springer, Berlin Heidelberg, pp 133–178Google Scholar
  34. Turcotte DL (1997) Fractals and chaos in geology and geophysics. Cambridge University Press, CambridgeCrossRefGoogle Scholar
  35. Vedanti N, Srivastava RP, Pandey OP, Dimri VP (2011) Fractal behavior in continental crustal heat production. Nonlinear Process Geophys 18(1):119–124CrossRefGoogle Scholar
  36. Waymire E (1989) On the main channel length-magnitude formula for random networks: a solution to Moon’s conjecture. Water Resour Res 25(5):1049–1050CrossRefGoogle Scholar